Poliedros que llenan el espacio son aquellos que al ponerlos unos junto a otros se tiene que no quedan espacios huecos entre ellos.
Decimos que esos poliedros forman una retícula espacial o también que hacen un cubrimiento del espacio.
Al igual que construimos redes mediante módulos planos, por ejemplo al anexionar distintos hexágonos como en los panales de miel de las abejas, podemos observar que se pueden unir unos hexágonos a otros sin dejar espacio ninguno para otro polígono.
En el caso del espacio sucede exactamente igual, podemos llenar el espacio al hacer una unión entre distintos poliedros o bien entre poliedros idénticos.
Una retícula espacial o cubrimiento del espacio se considera una forma de generalizar la retícula plana, aquello que aplicamos a los polígonos vale también en general para los poliedros, se trata de comprobar si rellenan el espacio sin dejar ningún intersticio entre ellos.
Hay analogías fáciles como el apilamiento de cubos en 3D, su correspondiente son cuadrados en 2D que se apilan perfectamente, si consideramos los cuadrados como proyecciones de cubos en planta, alzado y perfil, vemos que esta conformación es válida para las dos y tres dimensiones.
Aunque no siempre es tan fácil generalizar en el espacio ya que no siempre existen analogías entre el plano y el espacio, pasa por ejemplo con los triángulos equiláteros que también se pueden apilar de forma plana en una red modular, sin embargo su correspondiente, que sería el tetraedro regular, resulta imposible de apilar uno junto a otro y llenar el espacio; otra cosa es que tratemos de unirlo con otra figura como por ejemplo el octaedro regular, de esta manera sí que podemos llenar el espacio sin dejar huecos.
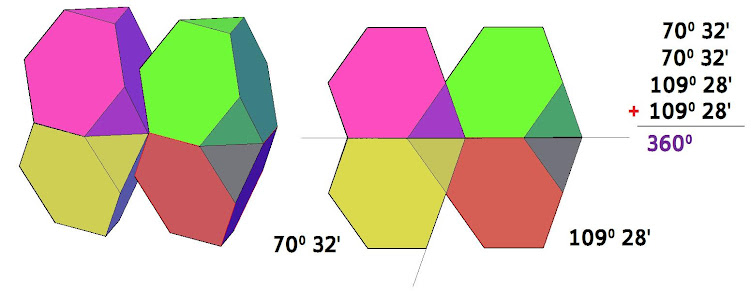
En la imagen tenemos los poliedros regulares, se define sobre ellos el ángulo que forman dos caras adyacentes, como los poliedros que llenan el espacio deben estar apilados unos junto a otros, vemos que esos ángulos al ser sumados con otros iguales no pueden llenar el espacio sin dejar huecos o sin solaparse entre ellos, salvo en el caso del cubo, pues 90º por 4 es 360° de ahí que podamos apilar cubos en el espacio sin dejar ningún hueco ni solapamiento.
En todo caso lo de los ángulos que cubren con exactitud el espacio es una condición necesaria para hacer un cubrimiento sin dejar huecos aunque no es una propiedad suficiente y lo vemos en el ejemplo siguiente.
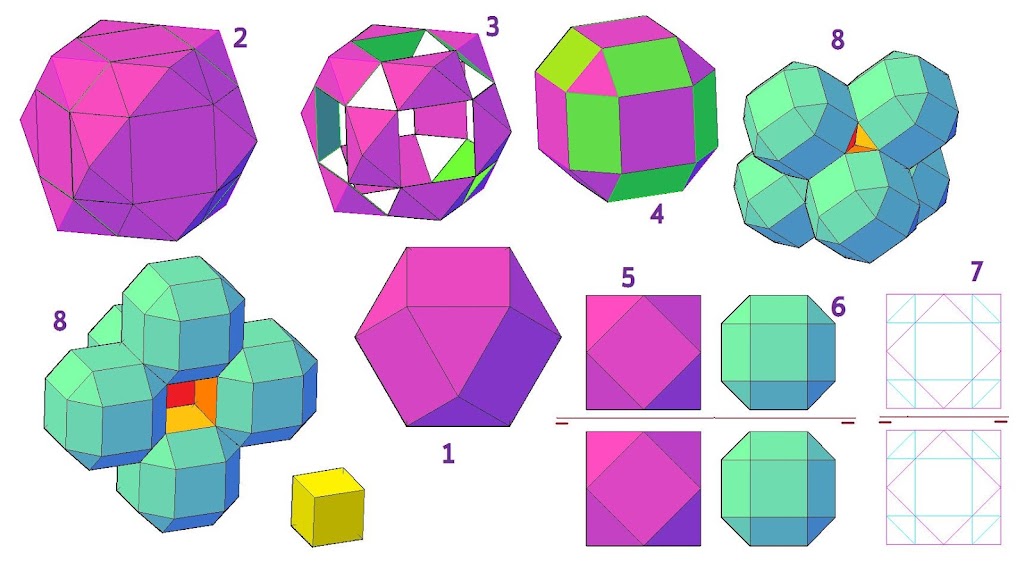
Observamos un poliedro arquimediano (Tetraedro truncado) que se obtiene a partir del truncamiento de tipo 2 (en 3 partes) del poliedro regular llamado tetraedro.
Como podemos observar en torno a una arista se pueden disponer las cuatro figuras de manera que cubren todo el espacio en ese tramo, pero si vemos las figuras en perspectiva observamos que no hay forma posible de colocar otros tetraedros truncados u otros regulares o semirregulares de manera que llenen el espacio sin dejar huecos.
Si forman 360º en torno a una arista ya tenemos una propiedad para que puedan cubrir el espacio sin dejar huecos aunque realmente no es una propiedad suficiente para que eso se cumpla, como vemos en este ejemplo.
A veces hay que apilar poliedros de distintas clasificaciones, regulares y arquimedianos, o incluso coger poliedros compuestos o estrellados. En todo caso es un tema incipiente en la geometría y con poca investigación con lo cual caben todavía muchas más propuestas, falta además una teoría que establezca pautas generales para la construcción y deducción de los mismos.
Octaedro regular
En el borde superior izquierdo observamos un
octaedro regular (poliedro que tiene 8 caras triangulares equiláteras de igual
tamaño) y un tetraedro regular ( poliedro que tiene 4 caras triangulares
equiláteras de igual tamaño).
Si ambas figuras se distribuyen de cierta
forma se pueden acoplar de manera que se llena el espacio sin dejar huecos,
inmediatamente debajo de las dos figuras de la izquierda observamos el octaedro
y debajo de éste, los cuatro tetraedros rodeados de octaedros, esa es la
disposición que debe adoptar cada una de las figuras. A su derecha observamos
la alineación de todos los tetraedros y cómo van encajando cada uno de los
poliedros en el centro de esas figuras, se han puesto además numerosas retículas para
poder observar con más detalle el acoplamiento.
En esta segunda imagen ya se ve de una manera
más ordenada el caso anterior.
A la izquierda observamos los cuatro tetraedros que
son simétricos 2 a 2 respecto al plano meridiano vertical y a su derecha los octaedros
que se acoplan en los huecos.
Como realmente la configuración no es muy intuitiva, se ha puesto en planta y alzado en el borde inferior derecho, la retícula modular que corresponde a los tetraedros en color rojo, mostrados en planta y alzado, mientras que a su izquierda observamos la alineación de los octaedros regulares. Como podemos observar en estos últimos los ejes centrales no están alineados en verticales como parecería que se da a entender a partir de la retícula roja, ello es debido a que los huecos que aparecen en planta en esta retícula no coinciden con los huecos de la planta inmediatamente superior.
Para
poder verlo con más claridad puede ser necesario construir una maqueta.
En la figura 1 observamos un rombododecaedro que es el poliedro dual del cuboctaedro, si cogemos los puntos mediosde las caras de éste obtenemos el cuboctaedro, la recíproca no es cierta.
En el número 2 tenemos dos líneas que pasan por los
centros de las caras y que se cortan en un vértice eso va a definir las
pirámides que deberemos montar sobre cada una de las caras en forma de rombo.
Los rombos no están constituidos por dos
triángulos equiláteros como podría parecer.
Una vez que prolongamos las dos caras verdes y
lo mismo con todas las caras obtenemos con la intersección, 4 planos que
corresponden a las caras laterales de una pirámide montada sobre la cara
superior tal y como se ve en el ejercicio 3.
En el ejercicio 4 muestra otra perspectiva y en
el 5 se intenta apoyar una pirámide de base cuadrada que por supuesto no
coincide con la base o con las aristas de la base de la figura.
Para poder construir de forma sólida esa pirámide deberemos extruir una cara del rombododecaedro o dodecaedro rómbico, tal y como aparece en el ejercicio 6 y una vez que tenemos el prisma recto a partir de ese rombo prolongamos las caras adyacentes y en la intersección de los planos obtenemos la pirámide como la que aparece en el número 7 en color azul.
En el número 10 aparece el dodecaedro rómbico sin la pirámide y en el número 11
otra perspectiva axonométrica de la pirámide con el poliedro.
Si aplicamos eso en todas las caras tendremos ya
el dodecaedro rómbico estrellado que aparece en la figura 15, 16 y 17, siempre
al lado del rombododecaedro para que se pueda observar las pirámides y las
bases que corresponden a las caras de la figura con igual orientación.
En el número 12 hemos puesto las tres vistas en
diédrico del dodecaedro rómbico estrellado, mientras que en el 13 las tres
vistas en su posición conforme para poderlas encajar en el poliedro anterior, el dodecaedro rómbico, como podemos observar el cuadrado del alzado
coincide con el cuadrado del alzado del dodecaedro rómbico estrellado.
Tenemos nuevamente el dodecaedro rómbico estrellado en sistema diédrico en el número 1, en el número 2 tenemos la figura que genera el dodecaedro rómbico estrellado a partir de la prolongación de sus caras, es el llamado dodecaedro rómbico, un poliedro de Catalan dual del cuboctaedro.
Podemos observar en la figura que aparte de las vistas en
diédrico tenemos la posición del cubo tal y como está en el número 4, con
el marcaje de las aristas mientras que en el número 3 tenemos el dodecaedro
rómbico sin las marcas del cubo.
En el número 12 tenemos el dodecaedro rómbico y
su estrellado en una posición conforme a las bases del poliedro
estrellado y coincidentes con las caras del dodecaedro rómbico.
En el número 11 observamos el poliedro
estrellado, es una disposición para que se vea la coincidencia de vértices y
aristas.
En el número 5, 6 y 7 aparecen las
perspectivas de las figuras correspondientes al 2, 3 y 4.
En el número 8 aparecen tres poliedros
estrellados mientras que en el 9 los hemos hecho coincidir con las cuatro
aristas de las pirámides que definen un plano, de esta manera se dejan huecos
para que se puedan encajar otros estrellados a sus alrededores tal y como se ve
en el número 10, efectivamente la cohesión de todos los estrellados
provoca el cubrimiento total del espacio sin dejar huecos.
El poliedro de la figura anterior, dodecaedro rómbico
o rombododecaedro también es una estructura que provoca el llenado íntegro del
espacio, en el número 1 y 2 vemos distintas disposiciones de la figura en las
vistas en diédrico, en el número 3 vemos distintas perspectivas axonométricas
del rombododecaedro, en el 4 ya podemos observar el apilamiento de los
distintos poliedros y cómo nos permite cubrir enteramente el espacio.
Es la única figura conocida en la que el mismo
poliedro y su estrellado cubre en el espacio.
Tenemos en el número 1 un octógono regular,
que es un polígono que tiene los lados y ángulos iguales, en total 8
lados. A partir de este polígono practicamos una elevación o extrusión
del mismo convirtiéndolo en un prisma recto a partir de la base 1. Una
vez que tenemos el prisma recto de color rojo que aparece en el número 2
hacemos dos copias y las giramos 90 grados en el espacio de manera que tenemos
los ejes longitudinales de las figuras coincidentes con los ejes
cartesianos, en disposición de un triedro trirrectángulo.
A continuación los superponemos de forma
centrada como en el número 3, luego calculamos la intersección y obtenemos el
poliedro que observamos en el número 4, formado por hexágonos irregulares y
cuadrados.
Si cortamos las esquinas donde se cortan los
hexágonos - figura 5- y quitamos las pirámides de base triangular
obtenemos la figura 7, en las 6 hemos puesto las pirámides
desplazadas de la figura para que se vea su distribución respecto al poliedro
que queda.
En el número 8 mostramos el poliedro del número
7 pero en un mismo color y en una axonometría trimétrica, para que no
coincidan caras con aristas y provoque de contorno un hexágono regular tal y
como aparece en el número 7.
Al apilar todos los poliedros obtenidos por el
truncamiento, llamados rombicuboctaedros, obtenemos una disposición como la que aparece en la Figura 9.
Hemos colocado en su interior un cubo centrado de manera que al quitarle al cubo los ocho rombicuboctaedros, obtenemos la figura del número 10, que es otro poliedro arquimediano al igual que el rombicuboctaedro pero formado por cuadrados y triángulos, es el llamado cuboctaedro, que aparece en la figura 11, una vez que se le han quitado los cubos.
En consecuencia podemos observar que el rombicuboctaedro y el
cuboctaedro junto con cubos llenan el espacio sin dejar intersticios.
Dipirámide cuadrangular elongada y cuboctaedro
Tomemos un cuboctaedro que es un poliedro arquimediano generado por la intersección del octaedro y del cubo, podemos juntar cuatro por sus caras cuadradas conforme a la figura 4, encima colocamos cuatro cubos sobre sus caras cuadradas horizontales y volvemos a colocar ahora sobre los cubos otros cuboctaedros.
Como podemos observar en la figura 4 el hueco que dejan estás 12 figuras es una dipirámide cuadrangular elongada, que es uno de los poliedros estudiados por Johnson, poliedros que abarcan a todos los convexos que tienen caras regulares después de descartar a los regulares, arquimedianos, prismas y pirámides.
En la en la Figura 1 podemos observar a la izquierda la planta y alzado de este poliedro de Johnson formado por dos pirámides de base cuadrangular conectadas por un cubo.
En la perspectiva se ve la pirámide superior que es realmente un semioctaedro regular ( la mitad de un octaedro regular).
Podemos ver también en la figura 1 un desarrollo (extensión de las caras sobre un plano en verdadera forma) de este poliedro de Johnson.
En la figura 2 podemos observar los cuboctaedros apilados con dos cubos, así podemos ver la pirámide hueca que queda en el centro y el cubo que se podrá formar a partir de los cubos apoyados en los cuboctaedro.
En la figura 3 podemos ver otra perspectiva de los cuboctaedros y los cubos y en el número 6, 7 y 5 observamos en tres dimensiones el poliedro de Johnson llamado dipirámide cuadrangular elongada.
En el número 1 tenemos un octaedro regular al que le
cortamos las esquinas por un truncamiento de tipo 2, es aquel que cortan las
aristas en tres partes de manera que en cada una de las caras sale un
polígono regular. Dependiendo de la base donde se apoya el nuevo polígono
podrá ser un polígono de distintos lados.
Una vez que le quitamos las esquinas al octaedro
tenemos en el número 2 el octaedro truncado (Poliedro de Kelvin), que es el anterior menos las
pirámides.
En el número 3 observamos distintas perspectivas
del octaedro mientras que en el 4,5,6 y 7 observamos
distintas proyecciones en diédrico del octaedro y del octaedro truncado.
En el número 4 la planta y alzado del octaedro
producen vistas iguales, también sería igual si pusiéramos el perfil, lo mismo
se puede decir en el número cinco del octaedro truncado, por estar hecho a
partir del truncamiento de la figura anterior también las tres proyecciones en
diédrico son iguales bajo esta disposición.
Si apoyamos el octaedro en una de sus caras
triangulares aparece como en el número 6 de manera que la planta tiene por
contorno un hexágono regular. La figura que se corresponde en planta para el octaedro truncado, por contorno tiene un polígono de 12 lados
aunque irregular.
Una vez que ya sabemos cómo se obtiene el
octaedro truncado podemos apilarlo junto a otros y obtener la configuración
del número 8 y del número 9, bajo distintas perspectivas axonométricas.
Este poliedro arquimediano llamado
octaedro truncado es también llamado poliedro de Kelvin.
En el número uno tenemos un cuboctaedro que es un
poliedro arquimediano que se obtiene directamente de dos poliedros regulares
mediante truncamiento de tipo 1, que es el que se produce al cortar la figura
por planos que pasen por mitad de cada una de las aristas.
Si cogemos un octaedro regular o su dual el
cubo, y los cortamos por los puntos medios de cada arista obtenemos esta figura
llamada cuboctaedro, esta es una propiedad de los poliedros duales, que
el truncamiento produce la misma figura.
Estos poliedros duales como todos los regulares
tienen una propiedad curiosa, si tomamos los puntos medios del cubo obtenemos
los vértices del octaedro regular, mientras que si tomamos los puntos medios
del octaedro regular obtenemos los vértices del cubo.
Una vez que tenemos ya el cuboctaedro como
truncamiento de cualquiera de los dos poliedros cubo u octaedro, los
podemos apilar de manera que juntemos sus caras cuadradas en franjas
horizontales, como podemos observar en el número 2, ahí nos queda una pirámide
hueca formada por 4 triángulos equiláteros, es la parte inferior del octaedro
regular, si hacemos la simétrica de estas cuatro figuras respecto al plano
superior obtendremos entonces como hueco el octaedro regular de forma completa.
Para intuir cómo serían los cuatro cuboctaedros apilados tenemos la figura 4, para ello imaginamos la figura 3 que giramos 180
grados y la superponemos sobre la figura 2 obteniendo la configuración del
número 4.
Sobre la figura 4 y el hueco de semi octaedro
regular, que aparece en el centro superior, hemos puesto una especie de desplazamiento del octaedro en su parte superior para que se entienda que
podríamos desplazar hacia abajo el poliedro hasta encajarlo en el hueco.
En consecuencia el cuboctaedro y el octaedro son
poliedros que también llenan el espacio sin dejar huecos.
Tenemos en el número uno un octógono irregular formado
por un lado de una unidad y el otro lado de un segmento cuya medida es raíz de
2 menos 1. Es el polígono que define el contorno de un cuboctaedro
truncado en cualquiera de las tres direcciones de los ejes cartesianos.
En el número 2 tenemos ese mismo polígono ya
en una axonometría trimétrica mientras que en el 3 hemos cogido el
mismo polígono y en axonometría isométrica lo hemos extruido hasta conseguir el
prisma azul del que hacemos dos copias y giramos 90 grados en el espacio para
obtener los otros dos prismas verde y rojo.
Al superponerlos como en la figura 4 obtenemos
la intersección de los tres en la figura 5, poliedro formado por cuadrados y
hexágonos irregulares.
En la figura 6 hemos marcado sobre sus caras los
cuadrados y hexágonos que van a definir el cuboctaedro truncado.
Para no tener que seccionar las 8 esquinas de
ese poliedro hemos cogido en el número 7 y le hemos cortado una única esquina,
colocando el poliedro truncado y su fragmento desplazado verticalmente.
En el número 8 hemos cogido, después de separar
el trozo, un octavo de la figura y nos queda lo que se llama un módulo del
poliedro, que quiere decir que podemos repetir esta forma un número de veces
con simetrías para obtener el cuboctaedro truncado del número 9. Para ello
deberemos hacer 3 simetrías para la configuración por encima del plano
meridiano y otra simetría para duplicar los cuatro trozos enlazados.
Una vez que tenemos el cuboctaedro truncado, que
es el poliedro arquimediano de la figura 9, lo apilamos tal y como aparece en
el número 10 en planta, hemos cogido ocho poliedros y lo hemos juntado, además
de marcar un cuadrado que define la posición de un cubo centrado con las cuatro
figuras.
Para entender mejor en el espacio esta
configuración hemos puesto en el 11 los cuatro cuboctaedros truncados con el
cubo de color amarillo que irá centrado dentro de los 8 poliedros.
En el número 12 aparecen ya a mayor tamaño los 8
poliedros con el cubo interior, al hacer una diferencia del cubo menos las
cuatro figuras obtenemos la configuración del número 13, es en realidad una
figura formada por un octaedro truncado y 6 cubos apoyados en sus caras
cuadradas, tal y como vemos en el número 14 después de practicar el
truncamiento.
Esto quiere decir que realmente el cuboctaedro
truncado junto con octaedros truncados y con los cubos, tenemos objetos espaciales que
llenan el espacio.
En la figura 1 tenemos tres prismas rectos de sección octogonal regular, sus generatrices siguen la dirección de los ejes cartesianos (triedro trirrectángulo), en el número 2 los hemos desplazado hasta centrarlos obteniendo la intersección de los 3 prismas en el número 3.
Como podemos observar es una figura formada por 4 hexágonos irregulares en la parte superior otros 4 laterales y otros 4 en la parte inferior, en total 12. Tenemos además 2 cuadrados, uno en la parte superior y otro en la inferior y 4 laterales, coincidentes todos con las caras de un cubo que lo inscriba, en total 6 cuadrados.
Al agruparlos como en la figura 4 de manera que hagamos coincidir sus caras hexagonales, podemos llegar a agrupar seis poliedros de manera que llenan todo el espacio si en el medio ponemos un cubo, tal y como se ve en la figura 6, en la que hemos puesto cinco poliedros para dejar ver el hueco cúbico y al lado el cubo en color magenta que se podría desplazar y encajar en el hueco. Recíprocamente podemos coger el cubo y sobre cada una de sus caras apoyar los 6 poliedros de manera que llenaríamos el espacio.
Para dar una mejor idea de la composición en el número 5 mostramos tres poliedros con el cubo en la parte superior y si hacemos los simétricos de esos tres obtendremos los 6 poliedros que engloban al cubo.
Parecido al rombicuboctaedro
En el número uno tenemos un cuboctaedro que es un poliedro arquimediano obtenido a partir del truncamiento de un poliedro regular que puede ser el cubo o el octaedro, ambos son poliedros duales por lo que al cortarlos por un corte de tipo 1 (por mitad de las aristas) se obtiene este poliedro.
Si tomamos el cuboctaedro del número 2 y le cortamos las esquinas por un corte de tipo 1, que es aquel que pasa por la mitad de las aristas, obtenemos el poliedro del número 4. Este poliedro está formado por cuadrados, triángulos equiláteros y rectángulos, tenemos en la franja superior 1 cuadrado, 4 rectángulos y 4 triángulos, en la inferior lo mismo y por la parte central tenemos 4 cuadrados y 4 rectángulos, en total 6 cuadrados, 8 triángulos y 12 rectángulos.
En el número 3 observamos las pirámides iguales que quedan al quitar el cuboctaedro.
En el número 5 vemos el cuboctaedro en planta y alzado mientras que en el 6 vemos el poliedro resultante del truncamiento. En el número 7 vemos ambos poliedros en forma alámbrica, de esta manera podemos observar cómo coinciden los puntos para su construcción, de hecho el cuadrado central del poliedro 6 tiene los vértices en los puntos medios de los cuadrados, de ahí su fácil construcción.
En el número 8 podemos observar cómo apilados en grupos de 6 podemos llenar el espacio dejando un cubo en el centro de las seis figuras, en el dibujo aparecen cinco para que se muestre el interior cúbico en color anaranjado mientras que se ve el cubo desplazado que se podría encajar en el hueco.
Si nos fijamos en las esquinas del cubo aparecen formas triangulares que construirían un tetraedro regular, eso quiere decir que rodeando a los cubos deberemos poner en sus esquinas 8 tetraedros regulares para poder llenar el espacio. En el número 8 se ve cómo se deben montar los tetraedros en las esquinas de 3 poliedros apilados.
Cuboctaedro truncado más tetraedro y cubo truncados
El cuboctaedro truncado es un poliedro arquimediano de 12 caras cuadradas, 8 hexagonales y 6 octagonales, todos polígonos regulares que suman en total 48 vértices y 72 aristas.Es un poliedro que lo podemos obtener por varios truncamientos a partir del cubo.
En la figura se agrupan varios cuboctaedros truncados de manera que los poliedros son unidos en sus caras cuadradas, de esta manera podemos observar que el agrupamiento de cuatro cuboctaedros truncados del dibujo 1, nos deja ver las caras de un cubo truncado, también nos deja ver un hueco triangular que puede ser la cara de un tetraedro truncado.
En el número 2 le hemos dado la vuelta a esos cuatro poliedros y podemos ver en color azul el hueco que deja en el que encaja un tetraedro truncado.
Una vez que tenemos los dos agrupamientos bajo distintos puntos de vista podemos en el número 3 ver exactamente lo mismo que en el 1 pero marcado en color rojo las caras octogonales donde va encajado el cubo truncado, que también es un poliedro arquimediano.
El cubo truncado se muestra en el número 4 mientras que en el número 5 mostramos la misma perspectiva que en el 2 pero hemos señalado en amarillo las caras hexagonales que corresponden al tetraedro truncado, poliedro arquimediano consistente en un tetraedro al que se le cortan las esquinas de manera que las caras resultantes son polígonos regulares.
En el número 6 vemos el tetraedro regular y la disposición para que encaje en los poliedros del número 5.
Como el conjunto de cuboctaedros truncados encierran la figura interior y no es fácil ver los huecos que provocan, hemos realizado el caso contrario, en el número 7 agrupamos los cubos truncados y la posición de los tetraedros truncados respecto a los mismos, podemos observar en el hueco la configuración del cuboctaedro truncado. En este número 7 mostramos con sólidos lo que en el número cinco eran huecos y recíprocamente.
Vamos a llenar el espacio con cubos truncados. Para hacer un cubo truncado se practica un corte en cada esquina, para practicar ese corte es necesario dividir la arista en tres partes aunque no iguales.
Ello es debido a que en cada cara va a quedar un polígono regular de 8 lados, y entre ellos quedará la base de la pirámide cortada que es un triángulo equilátero, pues el poliedro obtenido por truncamiento a partir del cubo es un poliedro arquimediano y como tal tiene todas sus caras que son polígonos regulares, esto es, polígonos con lados y ángulos iguales.
El método de dividir en tres partes una arista para proceder al truncamiento sería válido solo cuando cogemos un triángulo equilátero, al dividirlo en tres partes obtendremos sobre su cara un hexágono regular, ya que los lados del hexágono son iguales a la arista que contempla el triángulo equilátero que lo contiene.
Procedemos entonces como en el número 1 a dibujar dos octógonos regulares en planos verticales y marcamos la posición de sus aristas que van a definir el truncamiento. En el número 2 vemos el cubo que va a ser un cuarto de la figura y al que ya se le ha separado la pirámide de base triangular equilátera y lados laterales iguales. En el número 3 tenemos el poliedro arquimediano llamado cubo truncado. Aplicamos en el un corte de tipo 2 que es cuando las aristas se dividen en tres partes - en este caso no iguales como ya referimos anteriormente-, mientras que el corte llamado de tipo 1 del cubo producirá un cuboctaedro, al igual que si cortamos un octaedro regular, de ahí el nombre.
El cubo truncado aparece en planta, alzado y perfil en el número 13 mientras que en el 14 también aparece en las mismas vistas pero en este caso se apoya en un triángulo mientras que en el otro se apoya en el octógono.
Imaginamos como en el número 7, 8 cubos truncados apilados de esa forma ordenada y en el número 8 tenemos un cubo que vamos a centrar con las otras cuatro figuras.
De esta manera tendremos como aparece en el número 9, los 4 poliedros con el cubo centrado según se ve en planta, en el número 10 hemos puesto todos los cubos y hemos quitado uno de ellos para que se vea dónde va el cubo colocado respecto a los 8 cubos truncados.
Nos imaginamos muchos más cubos apilados como en el número 4 y en el número 5, al montar estos últimos sobre los anteriores tendremos la versión 6.
Si volvemos al número 10 y cogemos el cubo y aplicamos la diferencia del mismo sobre los 8 cubos truncados tendremos como en el número 11, un poliedro regular llamado octaedro regular, es un poliedro que tiene 8 caras que son triángulos equiláteros y cuyas distancias entre vértices opuestos son iguales.
Por último podemos ver en el número 12 los 8 cubos separados de cuatro en cuatro que dejan ver algunos octaedros regulares en color magenta entre ellos para llenar el espacio, como podemos ver el poliedro arquimediano amarillo y el regular magenta llenan el espacio sin dejar huecos.
Cuboctaedros, tetraedros truncados y octaedros truncados
En el número 1 vemos un octaedro truncado en color amarillo en cuyas caras hexagonales regulares se apoyan tetraedros truncados en color azul. Como tiene 8 caras que son hexágonos regulares está rodeado de 8 tetraedros truncados.
En el número 2 observamos el mismo octaedro truncado pero ahora sobre sus caras cuadradas se apoyan cuboctaedros de color magenta.
Podemos juntar los cuboctaedros y los tetraedros truncados sobre el octaedro truncado y llenar el espacio sin dejar huecos.
En el número 3 aparecen ambas conjuntos de agrupaciones con desplazamiento de los poliedros menores, lo que llamamos un despiece.
Volvemos a repetir lo mismo en la figura 4 pero marcando las caras visibles de la perspectiva y en color naranja para los tetraedros truncados y en azul para los cuboctaedros, ambos tienen contacto con el octaedro truncado.
En el número 2 observamos proyecciones ortogonales de ambas composiciones, están dispuestas de manera que se pueda entender mejor el encaje de las agrupaciones.
Tenemos la misma composición de poliedros que en el ejercicio anterior, en el número uno observamos el octaedro truncado con los tetraedros truncados sobre sus caras hexagonales, hemos dejado en color naranja y rojo los hexágonos a los que todavía no se les ha incorporado los tetraedros truncados.
En el número 2 tenemos el octaedro truncado con el grupo de cuboctaedros.
En el 3 tenemos una disposición que facilita la comprensión de el grupo de poliedros, una alineación que consiste en que el tetraedro truncado apoya su cara hexagonal en el octaedro truncado mientras que el cuboctaedro la apoya en el tetraedro truncado. En el 4 observamos cómo se disponen los poliedros, vemos que los octaedros truncados tienen en contacto las aristas intersección de dos hexágonos adyacentes. A partir de esta distribución se podría montar la estructura modular que llena el espacio como en el número 5, 6 y 7.
En el 7 vemos la disposición que deja el hueco del octaedro truncado, al igual que en el número 5.
En la izquierda del dibujo observamos 12 octaedros, 4 en en color amarillo en la parte superior, otros 4 inmediatamente debajo en color verde, de manera que tienen los vértices coincidentes, inferior y superior respectivamente, y por último 4 octaedros regulares en color rojo, de manera que cada uno tiene dos aristas coincidentes con dos octaedros amarillos y otras dos aristas inferiores coincidentes con dos octaedros verdes.
Si nos fijamos, esta estructura la podríamos volver a repetir quitando los rojos, que ya nos valdrían para la siguiente red, por ejemplo si cogemos otros 8 octaedros, cuatro amarillos más 4 verdes en posición idéntica y los copiamos y desplazamos a la derecha dejando el octaedro rojo, ya solo tenemos que coger los otros 3 octaedros rojos para distribuirlos alrededor, de esta manera podríamos seguir repitiendo esta forma aprovechando octaedros rojos.
En este conjunto de octaedros que hemos agrupado podemos entender que en su interior hay un hueco, para saber qué forma tiene ese hueco podemos ver el dibujo de la derecha, hemos cogido nuevamente los 12 octaedros y considerándolos como un grupo los hemos cortado por un plano meridiano de manera que el plano solo intercepta sólidamente a 2 octaedros rojos, cuya sección aparece en azul, a otros 4 octaedros el plano de corte los toca en una de sus aristas, por lo que toca 8 aristas.
El hueco que generan estos 12 octaedros es una estrella octángula u octangular de Kepler, figura azul que aparece en el centro y que está formada por dos tetraedros regulares centrados y dispuestos en una simetría central, también la podríamos construir a partir de un octaedro regular centrado en el que colocamos un tetraedro en cada una de sus caras de manera que externamente aparecen 8 tetraedros.
Como podemos ver esta estrella encaja en el interior de la configuración de 12 tetraedros octaedros sin dejar huecos, una de las caras del tetraedro corresponde a la zona naranja que se ve en el interior, esta zona naranja está interrumpida por un hueco en forma de tetraedro en el que se ve una cara roja y otra cara violeta, como podemos ver las caras rojas corresponden a caras de los tetraedros mientras que las violetas corresponden a otras caras de los tetraedros regulares.
En conclusión, podemos llenar el espacio con esta estructura formada por 12 dodecaedros que dejan en el interior una estrella octángula u octangular de Kepler, podemos seguir repitiendo esta forma y aprovechando algunos octaedros rojos para las configuraciones de octaedros que están anejas a está estructura básica.
Poliedros irregulares
Podemos construir infinitas variedades de poliedros que llenan el espacio si no imponemos como requisito que los poliedros tengan polígonos regulares.
En la figura número 1 tenemos un cubo con un eje que atraviesa dos aristas opuestas por el punto medio, al hacer el giro del cubo en una vuelta completa y dejar registro de 3 cubos en ángulos iguales de 120º tenemos la figura 2.
La intersección de los tres cubos provoca la figura 3, 4 y 5, en distintas perspectivas, estas figuras las podemos apilar como en el número 6 de manera que están unidas por sus hexágonos irregulares laterales; como podemos observar por cada tres poliedros se define sobre los mismos tres caras iguales que son deltoides unidos dos a dos por sus lados iguales, tal y como aparece en la figura 8, se observan tres deltoides rojos, tres verdes, tres azules, etc.
En la figura 7 hemos cogido estos poliedros objeto de la intersección y los hemos apilado en cuatro unidades en la base y en la parte superior se pueden observar tres, como podemos observar los de la base y los de la parte superior están unidos por sus vértices, el hueco que provocan 6 poliedros de este tipo está formado entonces por una figura que tiene 3 deltoides en la parte inferior, otros 3 deltoides en la parte superior y 3 caras laterales que son rombos, tal y como se observa en el número 10, según la disposición que encajaría en los poliedros apilados del número 6.
En consecuencia podemos deducir que por cada tres poliedros en la parte inferior y otros tres poliedros en la parte superior formamos uno en su parte central que es el que llena el espacio con los 6 anteriores.
En el número 9 se ven tres perspectivas distintas de este nuevo poliedro que rellena los huecos del poliedro conformado por la intersección de 3 cubos.
En el número 13 observamos las tres proyecciones en s. diédrico de la intersección de los tres cubos, es una figura formada por 6 hexágonos irregulares y 12 deltoides que se enlazan con esos hexágonos regulares laterales, de manera que los hexágonos dividen a la figura en 6 deltoides de un lado y otro 6 de otro.
Como podemos observar en la figura 13 en el perfil tenemos un hexágono regular como contorno de la figura mientras que en el alzado tenemos un hexágono irregular en verdadera forma.
Si ahora tomamos la figura 10 que es el poliedro que rellena los huecos, podemos obtener sus vistas en diédrico en el número 11 y 12, colocados según distintas disposiciones, en las vistas en diédrico se puede observar claramente que está formado por seis deltoides y tres cuadrados, en el número 12 en planta aparece un rombo en verdadera forma.